一、数组基础理论
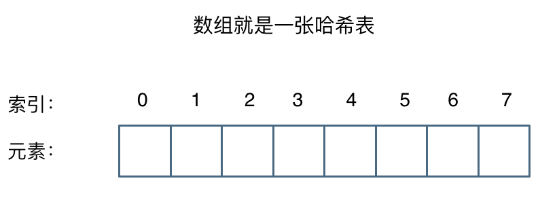
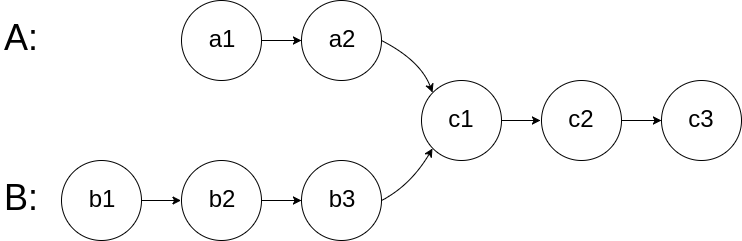
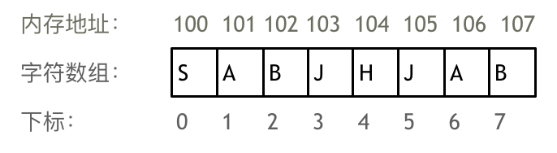
数组在内存中的存储方式:数组是存放在连续内存空间上的相同类型数据的集合,数组可以方便的通过下标索引的方式获取到下表对应的数据。
⭐注意:
- 数组下标都是从0开始的;
- 数组内存空间的地址是连续的
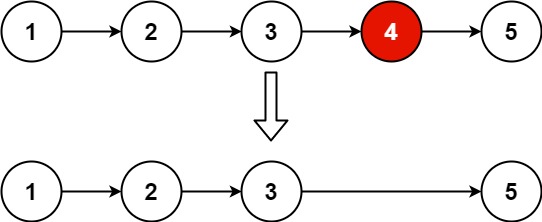
- 因为数组在内存空间的地址是连续的,所以我们在删除或增添元素的时候,就难免要移动其他元素的地址。
- 数组的元素是不能删除的,只能覆盖。
如删除下标为3的元素,需要对下标为3的元素后面的所有元素都要做移动操作:
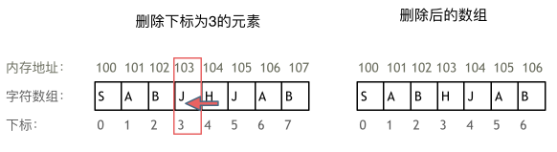
同时还要注意vector和array的区别:
vector的底层实现是array,严格来讲vector是容器,不是数组。
- vector是动态数组,可以动态增加和删除元素,但是vector的内存空间是不连续的,所以vector的访问效率没有array高;
- array是静态数组,内存空间是连续的,所以array的访问效率高,但是array的大小是固定的,不能动态增加和删除元素。
- vector和array都是C++的STL容器,vector是动态数组,array是静态数组。
- vector和array都是通过下标索引的方式访问元素。
- vector和array都是通过迭代器的方式遍历元素。
二维数组:
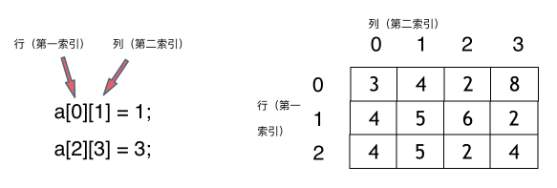
Q: 二维数组在内存的空间地址是不是连续的?
A: 是的!
写段代码验证一下:
#include <iostream>
using namespace std;
void test_arr() {
int array[2][3] = {
{0, 1, 2},
{3, 4, 5}
};
cout << &array[0][0] << " " << &array[0][1] << " " << &array[0][2] << endl;
cout << &array[1][0] << " " << &array[1][1] << " " << &array[1][2] << endl;
}
int main() {
test_arr();
}运行结果:
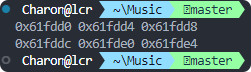
在Java中,我们不能像在C++中那样直接获取变量的内存地址。这是因为Java的设计哲学之一就是抽象化内存管理,让程序员专注于开发,而不是内存管理。Java的垃圾收集器会自动处理内存释放,所以我们无法直接访问或操作内存。
二、相关题目
2.1 二分查找
1.leetcode 704题:二分查找
原题链接: 704. 二分查找
给定一个
n个元素有序的(升序)整型数组nums和一个目标值target,写一个函数搜索nums中的target,如果目标值存在返回下标,否则返回-1。示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1提示:
- 你可以假设
nums中的所有元素是不重复的。n将在[1, 10000]之间。nums的每个元素都将在[-9999, 9999]之间。
题解:
// 二分查找 给定一个n个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
public int search(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = (left + right) / 2;
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}一些思考:
mid该如何计算?
在大多数情况下,(right + left) / 2 的计算速度会比(right – left)/ 2 + left 更快一些。 原因如下:
- 加法操作通常比减法操作更快。在现代计算机体系结构中,加法指令的执行时间通常比减法指令更短。
- 对于(right – left)/2+1eft 来说,需要先计算 right -left ,然后除以2,最后加上 1eft 。这需要执行3个操作,相比之下(right + left)/2 只需要2个操作(加法和除法)
- 当 left 和 right 的值较大时,rigt -1eft 的计算可能会导致整型溢出的问题,需要额外的处理。而(right + left) / 2 不会有这个问题。 因此,在大多数情况下,使用(right + left) / 2 的方式计算区间中点会更加高效和稳定。不过,在某些特殊情况下,比如需要避免整型溢出,使用(right – left) / 2+ left 也是可以的。关键是要根据具体的应用场景和性能需求来选择合适的方法。
2.leetcode 35题: 搜索插入位置
原题链接:35. 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为
O(log n)的算法。示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums为 无重复元素 的 升序 排列数组-104 <= target <= 104
题解:
// 搜索查找插入位置 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
public int searchInsert(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = (left + right) / 2;
if (nums[mid] == target) {
return mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return left;
}一些思考:为什么最后的left就是要插入的位置?
这是因为当 left > right 时,循环结束,此时 left 的位置就是 target 应该被插入的位置。这是因为在最后一次循环中,target 要么大于 nums[mid],此时 left 被设置为 mid + 1;要么小于 nums[mid],此时 right 被设置为 mid – 1,left 保持不变。无论哪种情况,left 都会指向 target 应该被插入的位置。
3.leetcode 34题: 在排序数组中查找元素的第一个和最后一个位置
原题链接: 34. 在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组
nums,和一个目标值target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值
target,返回[-1, -1]。你必须设计并实现时间复杂度为
O(log n)的算法解决此问题。示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]示例 3:
输入:nums = [], target = 0
输出:[-1,-1]提示:
0 <= nums.length <= 105-109 <= nums[i] <= 109nums是一个非递减数组-109 <= target <= 109
题解:
// 在排序数组中查找元素的第一个和最后一个位置.给定一个按照升序排列的整数数组 nums,和一个目标值 target。 如果 target 在数组中出现,则返回它的第一个和最后一个位置,否则返回[-1, -1]。
public int[] searchRange(int[] nums, int target) {
int left = searchLeftIndex(nums, target);
int right = searchRightIndex(nums, target);
// 情况一 target 在数组范围的右边或者左边
if(left == -2 || right == -2) return new int[] {-1, -1};
// 情况三 target 在数组范围中,且数组中存在target
if(right - left > 1) return new int[] {left + 1, right - 1};
// 情况二 target 在数组范围中,且数组中不存在target
return new int[] {-1, -1};
}
// 如果rightIndex没有被赋值,说明target在数组范围的左边 如: [1, 2, 3, 4, 5] target = 0
public int searchRightIndex(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
int rightIndex = -2;
while(left <= right){
int mid = left + (right - left) / 2;
// 右边界就是第一个大于target的数 所以当nums[mid] == target时,我们要继续向右查找
// 当nums[mid] > target时,说明target在数组的左边,我们要继续向左查找
if(nums[mid] > target) {
right = mid - 1;
} else {
// 当nums[mid] < target时,说明target在数组的右边,我们要继续向右查找同时记录右边界
// 当nums[mid] == target时,我们要找的右边界就在mid的右边
left = mid + 1;
rightIndex = left;
}
}
return rightIndex;
}
// 如果leftIndex没有被赋值,说明target在数组的右边 如: [1, 2, 3, 4, 5] target = 6
public int searchLeftIndex(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
int leftIndex = -2;
while(left <= right){
int mid = left + (right - left) / 2;
// 左边界就是第一个大于等于target的数 所以当nums[mid] > target时,我们要继续向左查找
if(nums[mid] >= target) {
// 当nums[mid] == target时,我们要找的左边界就在mid的左边
right = mid - 1;
leftIndex = right;
} else {
// 当nums[mid] < target时,说明target在数组的右边,我们要继续向右查找
left = mid + 1;
}
}
return leftIndex;
}思考: 如何界定左右边界
- 如果 nums[mid] 大于等于目标值 target,则目标值可能在 mid 的左侧,因此将 right 设置为 mid – 1,并记录 leftIndex 为 right。如果 nums[mid] 小于目标值 target,则目标值在 mid 的右侧,因此将 left 设置为 mid + 1。
- 如果 nums[mid] 大于目标值 target,则目标值在 mid 的左侧,因此将 right 设置为 mid – 1。如果 nums[mid] 小于等于目标值 target,则目标值可能在 mid 的右侧,因此将 left 设置为 mid + 1,并记录 rightIndex 为 left。
这样,通过不断地调整左右边界并进行二分查找,最终可以找到目标值的左右边界。
4.leetcode 69题: x的平方根
原题链接: 69. x 的平方根
给你一个非负整数
x,计算并返回x的 算术平方根 。由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如
pow(x, 0.5)或者x ** 0.5。示例 1:
输入:x = 4
输出:2示例 2:
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。提示:
0 <= x <= 231 - 1
题解:
// 给你一个非负整数 x ,计算并返回 x 的平方根。由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
public int mySqrt(int x) {
// 初始化左边界为1,右边界为x
int left = 1;
int right = x;
// 初始化结果为-1
int ans = -1;
// 如果x为0或1,直接返回x
if (x == 0 || x == 1) {
return x;
}
// 当左边界小于等于右边界时,执行循环
while (left <= right) {
// 计算中间值
int mid = (left + right) / 2;
// 如果中间值的平方大于x,说明答案在中间值的左侧,将右边界设置为mid - 1,并更新结果为右边界
if (mid > x / mid) {
right = mid - 1;
ans = right;
} else {
// 如果中间值的平方小于等于x,说明答案在中间值的右侧,将左边界设置为mid + 1
// 如果mid + 1的平方大于x,说明mid为最接近x的整数平方根
if ((mid + 1) > x / (mid + 1)) {
return mid;
}
left = mid + 1;
}
}
// 返回结果
return ans;
}一些思考:
- 初始化左边界为0,右边界为x。
- 当左边界小于等于右边界时,执行以下操作:
- 计算中间值mid为左边界和右边界的平均值。
- 如果mid的平方小于x,那么我们知道答案肯定在mid的右侧,所以将左边界设置为mid+1。
- 如果mid的平方大于x,那么我们知道答案肯定在mid的左侧,所以将右边界设置为mid-1。
- 如果mid的平方等于x,那么mid就是我们要找的答案,直接返回。
- 当左边界大于右边界时,说明我们已经找不到一个完全平方数等于x,此时右边界就是最接近x的平方根的整数,返回右边界。
5.leetcode 367题: 有效的完全平方数
原题链接: 367. 有效的完全平方数
给你一个正整数
num。如果num是一个完全平方数,则返回true,否则返回false。完全平方数 是一个可以写成某个整数的平方的整数。换句话说,它可以写成某个整数和自身的乘积。
不能使用任何内置的库函数,如
sqrt。示例 1:
输入:num = 16
输出:true
解释:返回 true ,因为 4 * 4 = 16 且 4 是一个整数。示例 2:
输入:num = 14
输出:false
解释:返回 false ,因为 3.742 * 3.742 = 14 但 3.742 不是一个整数。提示:
1 <= num <= 231 - 1
题解:
// 有效的完全平方数 给定一个正整数 num,编写一个函数,如果 num 是一个完全平方数,则返回 True,否则返回 False。
public boolean isPerfectSquare(int num) {
// 如果num为0或1,直接返回true,因为0和1都是完全平方数
if (num == 0 || num == 1) {
return true;
}
// 初始化左边界为1,右边界为num
long left = 1;
long right = num;
// 当左边界小于等于右边界时,执行循环
while (left <= right) {
// 计算中间值
long mid = (left + right) / 2;
// 计算中间值的平方
long square = mid * mid;
// 如果中间值的平方等于num,说明num是一个完全平方数,返回true
if (square == num) {
return true;
} else if (square < num) {
// 如果中间值的平方小于num,说明答案在中间值的右侧,将左边界设置为mid + 1
left = mid + 1;
} else {
// 如果中间值的平方大于num,说明答案在中间值的左侧,将右边界设置为mid - 1
right = mid - 1;
}
}
// 如果循环结束还没有找到一个数的平方等于num,说明num不是一个完全平方数,返回false
return false;
}一些坑:
在判断中间值的平方是否等于num时 不能直接判断
if(mid == num / mid)这是因为由于整数除法的向下取整特性,mid 和 num / mid 可能会相等,但 mid * mid 并不等于 num。就比如 num = 5时。
- 初始化左边界为0,右边界为num。
- 当左边界小于等于右边界时,执行以下操作:
- 计算中间值mid为左边界和右边界的平均值。
- 如果mid的平方小于num,那么我们知道答案肯定在mid的右侧,所以将左边界设置为mid+1。
- 如果mid的平方大于num,那么我们知道答案肯定在mid的左侧,所以将右边界设置为mid-1。
- 如果mid的平方等于num,那么mid就是我们要找的答案,直接返回true。
- 当左边界大于右边界时,说明我们已经找不到一个完全平方数等于num,返回false。